
حل مکعب روبیک با پایتون
سلام به همه، امروز ما با استفاده از پایتون ۳، یک حل کننده مکعب روبیک ایجاد خواهیم کرد. در این نوشته، من به مرور بازیهای رایج و الگوریتمهای لازم برای حل هر نوع روبیک رو به شما آموزش میدهم.
با توجه به شهرت مکعب روبیک، مطمئنم که قبلاً یکی را دیدهاید، اما در صورتی که ندیدهاید، یک توضیح سریع ارائه میدهم. روبیک مکعب یک بازی محبوب اختراع شده توسط ارنو روبیک است. قوانین سادهای برای روبیک مکعب وجود دارد، از ترکیب پازل ۳ بعدی خلاص شوید. به طور سنتی، یک روبیک مکعب یک مکعب ۳x۳ است، اما اکنون بسیاری از نسخههای مختلف از بازی کلاسیک وجود دارند.
روبیک مکعبها پازلهای پیچیدهای هستند که برای حل کردن آنها با حدود 43،252،003،274،489،856،000 ترکیب ممکن مواجه هستیم.
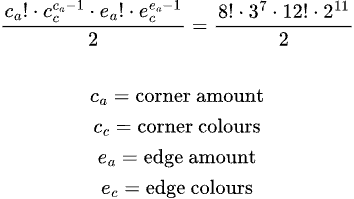
به دلیل این پیچیدگی، بسیاری از افراد از همهجا به مطالعه روبیک مکعب مشغولند، از علاقهمندان تا ریاضیدانان. ریاضیدانان به دلیل نظریه گروه پیچیدهی آن، به روبیک مکعب علاقهمند شدهاند و بسیاری مقالات علمی در این زمینه نوشتهاند.
یکی از مقالات بسیار مهم در این زمینه، مقاله “قطر گروه روبیک مکعب بیست است” است. در این مقاله، آنها مشخص کردند که “عدد خدا” برابر با ۲۰ چرخش است. “عدد خدا” یکی از مفاهیم روبیک مکعب است که به بیشترین تعداد چرخشهای ممکن برای حل کردن یک مکعب در هر شکلی اشاره دارد.
یکی دیگر از چیزهای قابل توجهی که از این مطالعه به دست آمده است، ایجاد الگوریتمهای استاندارد برای حل مکعب است.
ایجاد مکعب روبیک
حال که ما دانش پایهای در مورد روبیک مکعب داریم، قدم اول ما ساختن یک مکعب است. به دلیل سادگی، ما به مکعبهای nxn عمل خواهیم کرد تا نیازی به مربعهای دیگر یا شکلهای سه بعدی دیگر نداشته باشیم (گاهی اوقات پازل به شکلهای مثل مربعها یا مثلثها است).
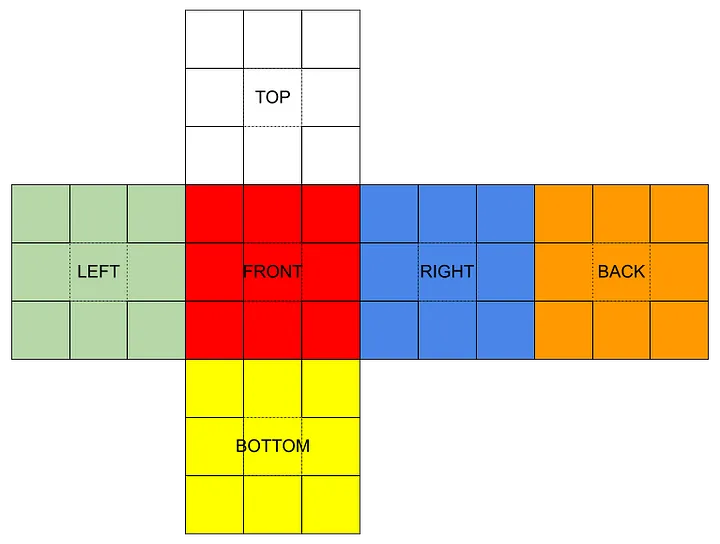
برای ساختن مکعب خود، بیایید یک کلاس سفارشی برای تعامل کاربر ایجاد کنیم. به این ترتیب، ما میتوانیم حالت داخلی را در شی مکعب خود ذخیره کنیم تا تعداد متغیرهای مورد نیاز برای هر تابع هنگام تلاش برای تغییر مکعب کاهش یابد.
ابتدا، باید ساختار دادهای موثرتر برای ایجاد مکعب خود تعیین کنیم. به دلیل ایجاد نیاز به تغییر مکعب، برای این پروژه از یک آرایه سه بعدی (فهرست تو در تو) استفاده خواهیم کرد. این ساختار دادهای را به دلیل تلاش برای تغییر مکعب انتخاب کردهام. با استفاده از یک آرایه سه بعدی، ما میتوانیم نگاشتهایی را برای جابجایی مربعها در مکان به طور میانگین در زمان O(n) ایجاد کنیم.
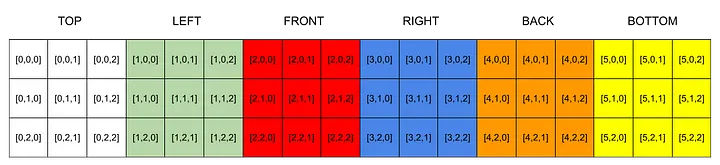
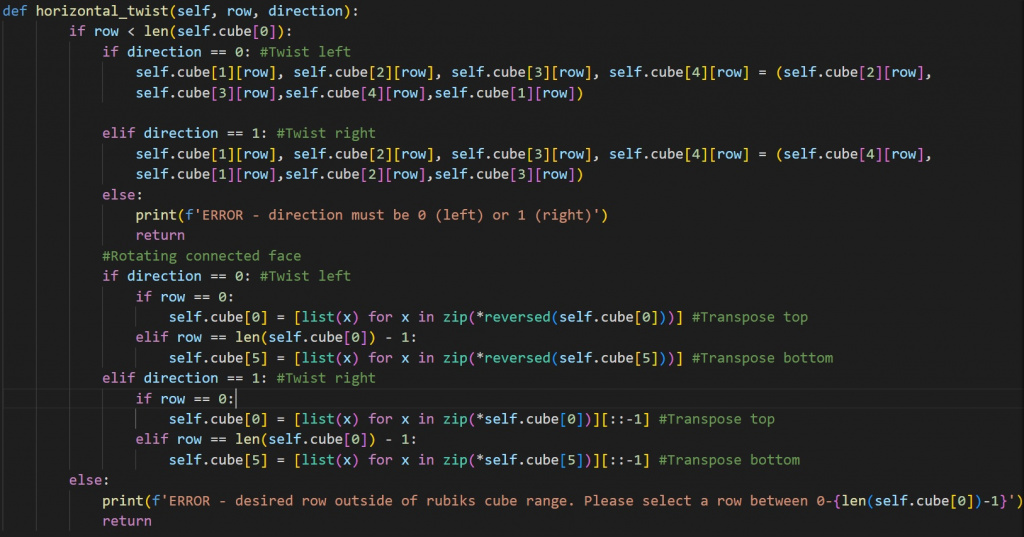
سپس، باید سه تابع مجزا برای تغییر مکعب بسازیم. در یک Rubik’s cube، تنها سه نوع حرکت ممکن هستند که میتوانید انجام دهید.
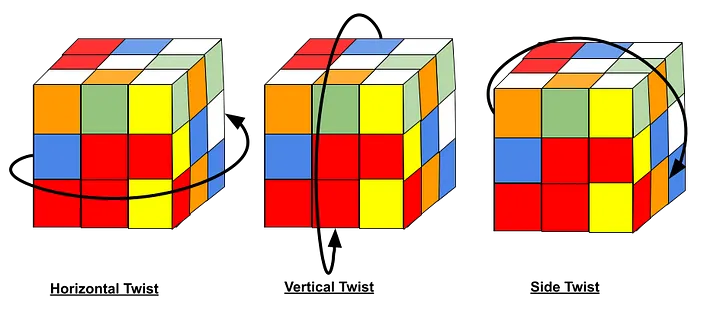
سه تابع حرکت ما رویکرد بسیار مشابهی دارند. ما از تصویرسازی استفاده میکنیم تا موقعیت مکعب ها را در جای خود تعویض کنیم. برای تابع توری و برگشتی کناری، از یک حلقه for استفاده میکنیم تا از هر ردیف ستون عبور کنیم، بنابراین این توابع یک پیچیدگی زمانی O(n) دارند. با این حال، تابع چرخش افقی ردیفها را در محل تعویض میکند که باعث میشود پیچیدگی زمانی آن O(1) باشد. همچنین، با هر چرخش، بررسی میکنیم که آیا باید صفحهی نزدیکتر را بچرخانیم یا نه. برای چرخش یک صفحه از Rubik’s cube، ما ماتریس مربوطه را ترانهاده میکنیم.
راه حل
حالا که یک مدل کارآمد از مکعب روبیک داریم، بیایید شروع به کار برای حل کننده کنیم.
برای حل کننده، چندین رویکرد میتوانیم به کار ببریم. با این حال، ما قصد داریم از رویکرد درخت بازی استفاده کنیم.
در رویکرد درخت بازی، ما میدانیم که برای پیدا کردن کمترین تعداد حرکات برای حل مکعب، نیاز به جستجوی درخت بازی داریم. میتوانیم از روش زوری استفاده کنیم، با این حال، با محدودیتهای محاسباتی امروز، این کار غیرممکن است. به جای آن، ما از یک الگوریتم جستجوی کارآمدتر استفاده خواهیم کرد.
الگوریتمی که قصد داریم استفاده کنیم الگوریتم جستجوی IDA* (Iterative Deepening A*) است. این الگوریتم به دلیل محدودیت حافظه، نسبت به A* انتخاب شده است. A* و IDA* از رویکرد مشابهی استفاده میکنند، که در A*، گرههای بازدید شده به یادگیری حافظهای هستند، در حالی که در IDA* اینطور نیست. به طور معمول، A* برای مسئله جستجوی بهینه استفاده میشود، با این حال، با این اندازهی فضای جستجو، احتمال زیادی وجود دارد که از حافظه تمام شود اگر از A* استفاده میکردیم.
IDA* یک روش جستجو درختی است که از ترکیب هیوریستیک و جستجوی عمق اول استفاده می کند. در IDA* هیوریستیک ها با جستجوی DFS راهنمایی می کنند و در هر بار گسترش درخت مشابه Monte Carlo Tree Search (MCTS) صورت می گیرد.
در زیر، یک درخت نمونه برای روش IDA* نشان داده شده است. در این نمودار، امتیاز g_score (هزینه رسیدن به گره فعلی) و امتیاز h_score (هزینه پیش بینی شده مسیر آینده) نشان داده شده است. این الگوریتم از جمع ساده امتیاز g_score و h_score برای ارزیابی هر گره استفاده می کند.
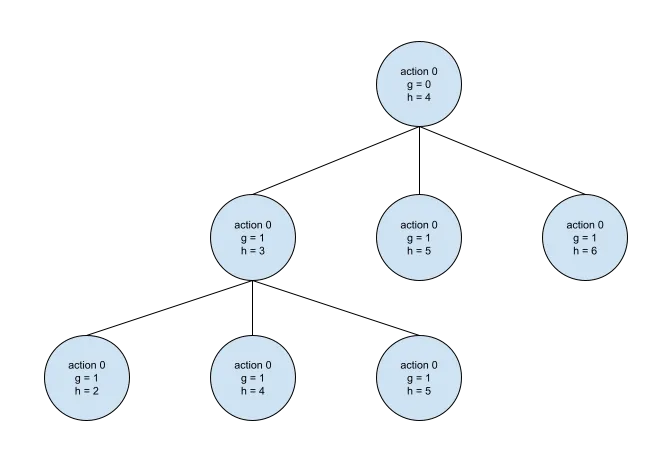
همانطور که قبلاً گفته شد، در IDA* ما از گرههای بازدید نشده یادداشت نمیگیریم. یادداشت نگرفتن گرههای بازدید شده مزایا و معایبی دارد. با یادداشت نگرفتن گرههای بازدید شده، احتمال دوباره بازدید از یک گره وجود دارد که باعث افزایش پیچیدگی زمانی الگوریتم کلی میشود. با این حال، با یادداشت نگرفتن گرههای بازدید شده، نیازی به حافظه کمتری داریم. برای مورد استفاده ما ذخیره کردن حافظه اهمیت دارد زیرا با یک درخت بازی حداکثر 43،252،003،274،489،856،000 گره سروکار داریم.
حال که درک بهتری از الگوریتمی که قرار است استفاده کنیم داریم، بیایید آن را بسازیم. اولین چیزی که باید انجام دهیم ساخت هیوریستیک ما است.
برای هیوریستیک خود، به یک رویکرد خام استفاده شده و از الگوریتم جستجوی اول عرض برای بررسی گرهها استفاده خواهیم کرد. در اینجا، ما وضعیتهای مختلف مکعب و تعداد حرکات مورد نیاز برای رسیدن به آن از مکعب حل شده را در یک جدول هش ذخیره خواهیم کرد. با ذخیره کردن وضعیتهای مکعب در یک جدول هش، یک جدول جستجوی ساده برای شناختن کدام وضعیت کمترین تعداد حرکت برای حل دارد، ایجاد کردهایم.
def build_heuristic_db(state, actions, max_moves = 20, heuristic = None):
if heuristic is None:
heuristic = {state: 0}
que = [(state, 0)]
node_count = sum([len(actions) ** (x + 1) for x in range(max_moves + 1)])
with tqdm(total=node_count, desc=’Heuristic DB’) as pbar:
while True:
if not que:
break
s, d = que.pop()
if d > max_moves:
continue
for a in actions:
cube = RubiksCube(state=s)
if a[0] == ‘h’:
cube.horizontal_twist(a[1], a[2])
elif a[0] == ‘v’:
cube.vertical_twist(a[1], a[2])
elif a[0] == ‘s’:
cube.side_twist(a[1], a[2])
a_str = cube.stringify()
if a_str not in heuristic or heuristic[a_str] > d + 1:
heuristic[a_str] = d + 1
que.append((a_str, d+1))
pbar.update(1)
return heuristic
حال که هیوریستیک ما را داریم، میتوانیم الگوریتم IDA* را برای حل کردن مکعب پیاده سازی کنیم. این الگوریتم از یک الگوریتم DFS (جستجوی عمقی) ساده با روش امتیازدهی توصیف شده در بالا (امتیاز g_score + h_score) استفاده میکند. در هر گره که با آن در حال بازدید هستیم، امتیاز g_score گره قبلی را ارسال خواهیم کرد تا هزینه فعلی را بدانیم. برای تعیین امتیاز h_score، با استفاده از یک lookup سریع از نود در جدول هیوریستیک خود این کار را انجام خواهیم داد. برای سادگی، اگر یک نود را پیدا نکردیم، امتیاز h_score را به 20 (عدد خدا) تنظیم خواهیم کرد. در اینجا ما میتوانیم معادلات اضافی ایجاد کنیم تا یک تخمین بهتر بگیریم، اما برای مورد استفاده ساده خود، این کار لازم نیست (اگر معادلهای برای این کار دارید، لطفاً آن را در نظرات بگذارید). با تمام اینها، چیزی شبیه کد زیر باید به دست بیاید.
def search(self, state, g_score):
cube = RubiksCube(state=state)
if cube.solved():
return True
elif len(self.moves) >= self.threshold:
return False
min_val = float(‘inf’)
best_action = None
for a in [(r, n, d) for r in [‘h’, ‘v’, ‘s’] for d in [0, 1] for n in range(cube.n)]:
cube = RubiksCube(state=state)
if a[0] == ‘h’:
cube.horizontal_twist(a[1], a[2])
elif a[0] == ‘v’:
cube.vertical_twist(a[1], a[2])
elif a[0] == ‘s’:
cube.side_twist(a[1], a[2])
if cube.solved():
self.moves.append(a)
return True
cube_str = cube.stringify()
h_score = self.heuristic[cube_str] if cube_str in self.heuristic else self.max_depth
f_score = g_score + h_score
if f_score < min_val:
min_val = f_score
best_action = [(cube_str, a)]
elif f_score == min_val:
if best_action is None:
best_action = [(cube_str, a)]
else:
best_action.append((cube_str, a))
if best_action is not None:
if self.min_threshold is None or min_val < self.min_threshold:
self.min_threshold = min_val
next_action = choice(best_action)
self.moves.append(next_action[1])
status = self.search(next_action[0], g_score + min_val)
if status: return status
return False








برای نوشتن دیدگاه باید وارد بشوید.